| Contributors |
|
Reduced CA3 cell model from Pinsky & Rinzel 1994¶
Overview of the Model¶
The Pinsky and Rinsel (1994) model is a 2-compartment (soma and dendrite), conductance-based (Hodgin-Huxley type) model of a hippocampal CA3 pyramidal neuron. It is a reduced version of an earlier, 19-compartment model by Traub, et. al. (1991). This model demonstrates how similar qualitative and quantitative spiking behaviors can be obtained despite the reduction in model complexity.
Demonstrated Physiological Properties¶
Specifically, this model demonstrates calcium bursting behavior and how the 'ping-pong' interplay between somatic and dendritic currents results in a complex shape of the burst.
Model Versions¶
Why Convert to NeuroML?¶
The original model was implemented for the XPP simulator. We have converted the model to NeuroML. The modular, XML nature of NeuroML allows to quickly re-use this model in network simulations and our tools allow automated conversion to other supported simulator formats.
NeuroML2/LEMS Versions¶
The model has been implemented as a new ComponentType in LEMS. There is one version which uses dimensional quantities for all parameters and voltage (pinskyRinzelCA3Cell.xml) and one that uses dimensionless parameters/variables (pinskyRinzelCA3CellDL.xml). These ComponentTypes will eventually be incorporated into the core NeuroML2 ComponentType definitions.
The aforementioned ComponentTypes contain all parameters, derived variables etc. for the model in a single Component. There is also a hierarchical version of the model using more of the NeuroML2 types for segments, channels etc.
Installation Instructions¶
Download the Model Files, or clone the repository using git:
git clone https://github.com/OpenSourceBrain/PinskyRinzelModel.git
Follow instructions to Install jNeuroML for the jnml executable. On Windows, you may also need SVN. Alternatively install PyNeuroML for the pynml executable.
Set the $PATH and $JNML_HOME variables as described in #2
Extract the model files to a folder. Change to NeuroML2/LEMS.
For Figure 2: Type
jnml LEMS_Figure2.xmlorpynml LEMS_Figure2.xml.For Figure 3: Type
jnml LEMS_Figure3.xmlorpynml LEMS_Figur3.xml.Windows with the plotted figures should show up as can be seen below.
Demonstrated Properties¶
Figure 2¶
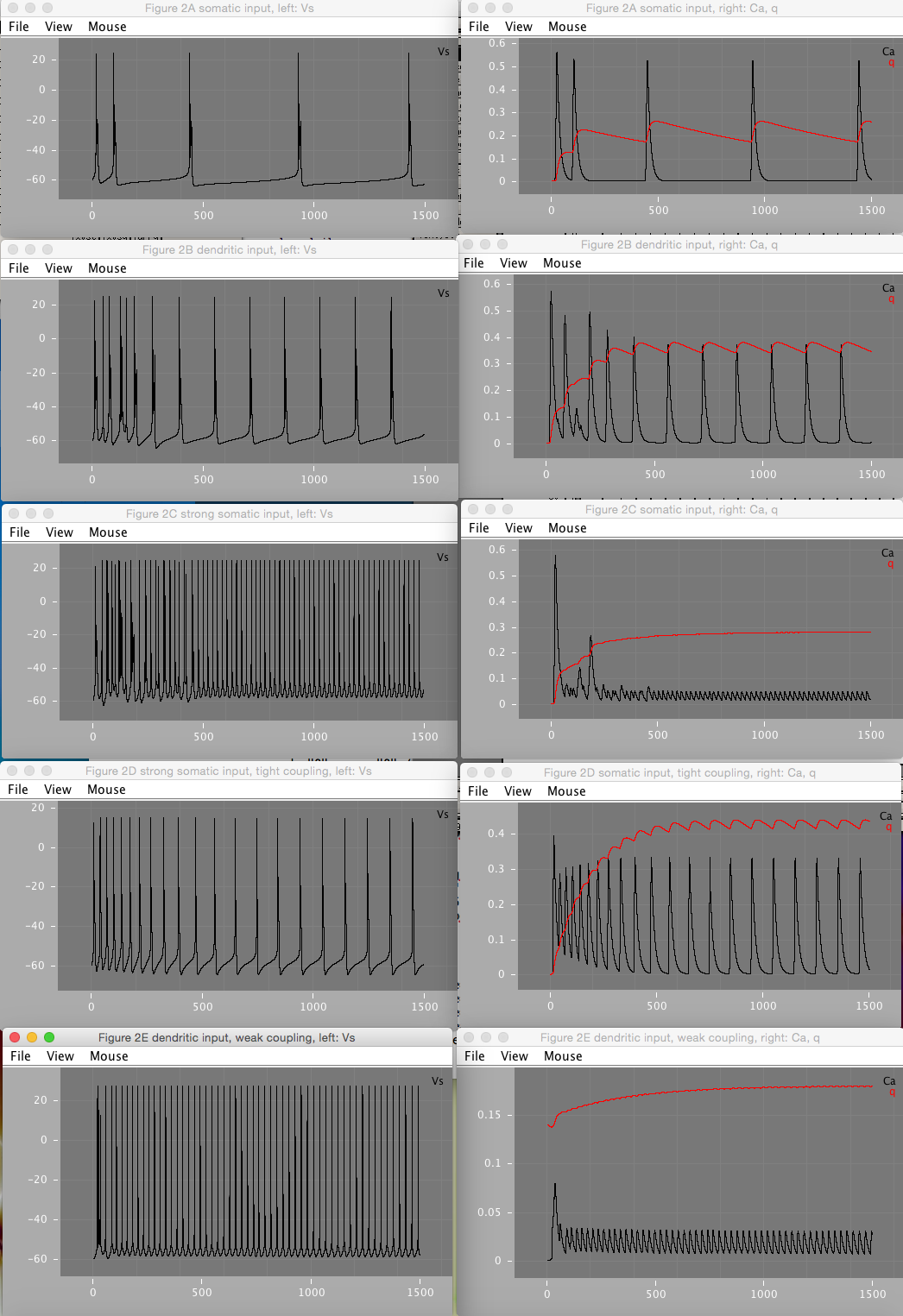
Figure 2 shows how various amounts of current injection into the soma (Figure 2A, C, and D) and dendrite (Figure 2B and E) compartments, under varying coupling strengths affects the soma firing pattern. Figure 2D shows that under tight coupling, the model approximates a single-compartment model and does not result in bursts.
Figure 3¶
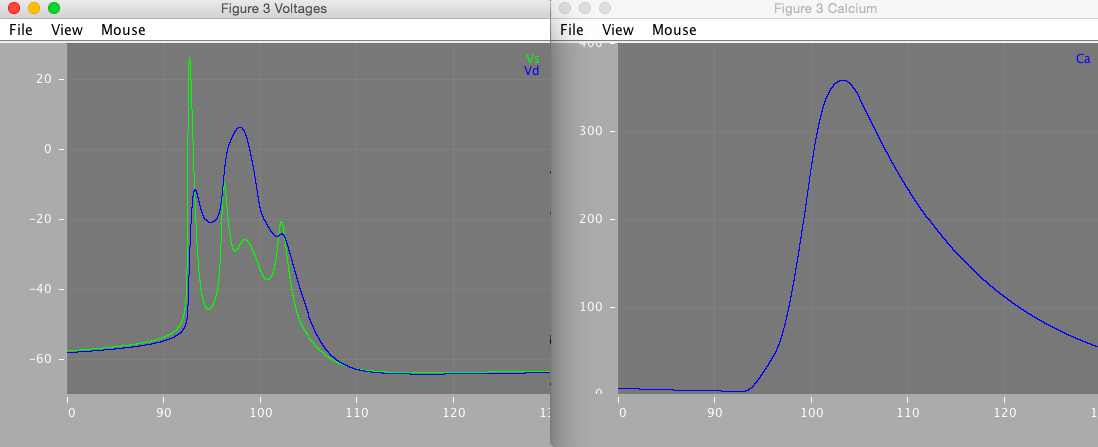
Figure 3 is a close-up of the second burst in figure 2A. It demonstrates how the complex burst shape emerges from the 'ping-pong' interplay of the somatic and dendritic currents.
Other Versions¶
There are several versions of the model:
- Original: The original version made for the XPP simulator was obtained from ModelDB.
- Original with Synaptic Dynamics: The original file did not contain the dynamics for synaptic currents described in the paper. These have been re-implemented and added.
- Dimensionless LEMS: The original model with synaptic dynamics implemented in LEMS (XML files runnable using jNeuroML).
- LEMS with Dimensions: Same as Dimensionless LEMS, but implemented with the units specificied in the original paper.
- Two-Compartment NeuroML2: This is the LEMS with Dimensions model expressed in NeuroML.
Issues¶
Figure 2B¶
Figure 2B is mostly reproducible. gnmda parameter (2nd of the triple in figure caption) appears to be mislabeled, and seems to be closer to Id(endrite) than gnmda. Varying gnmda parameter has no effect on the Vs, Ca, or q variables depicted in the figures. Varying Id, results in a closer match, and is also more consistent with the written description of dendritic stimuation mentioned in the figure. Varying Id, the closest match to 2B as depicted in the figure occurs when Id = 2.0 mA.
Figure 2E¶
Figure 2E is reproducible only partially. Assuming gnmda refers to Id (see above figure 2B issue), and varying Id values, the closest match occurs around Id = 2.0 mA. Furthermore, initial value of qd = 0.4, as described in the paper, appears to be incorrect. Setting initial value to 0.14 results in a closer match. The paper describes that figure 2E spiking pattern was a periodic pattern of a burst followed by a spike. However, no combination of values of gc, Id, Is, gnmda, or initial qd was found to reproduce this pattern in XPP or LEMS. Furthermore, at Is=-0.5, Id=2, and varying gc around 1.425 (as mentioned in paper), the spiking pattern becomes very sensitive to small changes in gc. Because the paper describes a chaotic pattern, the spikes are very sensitive to the value of gc, and several parameter values appear to be incorrect, it's possible the reported figure is unreproducible without additional or existing paremeters being specified more precisely.
Figure 3¶
Figure 3 matches the published figure very closely, however some small differences in the precise shapes of the membrane potential traces remain.
Differences between LEMS and twoCompartment versions¶
The spike times for the LEMS with Dimensions and Two-Compartment NeuroML2 are very close but not identical (<1ms differences for runs <100 ms, 1-5ms differences for runs >1000 ms). This appears even if the models are simplified down to a single equation. Reported as https://github.com/OpenSourceBrain/PinskyRinzelModel/issues/13.
Reusing this model¶
The code in this repository is provided under the terms of the software license included with it. If you use this model in your research, we respectfully ask you to cite the references outlined in the CITATION file.


